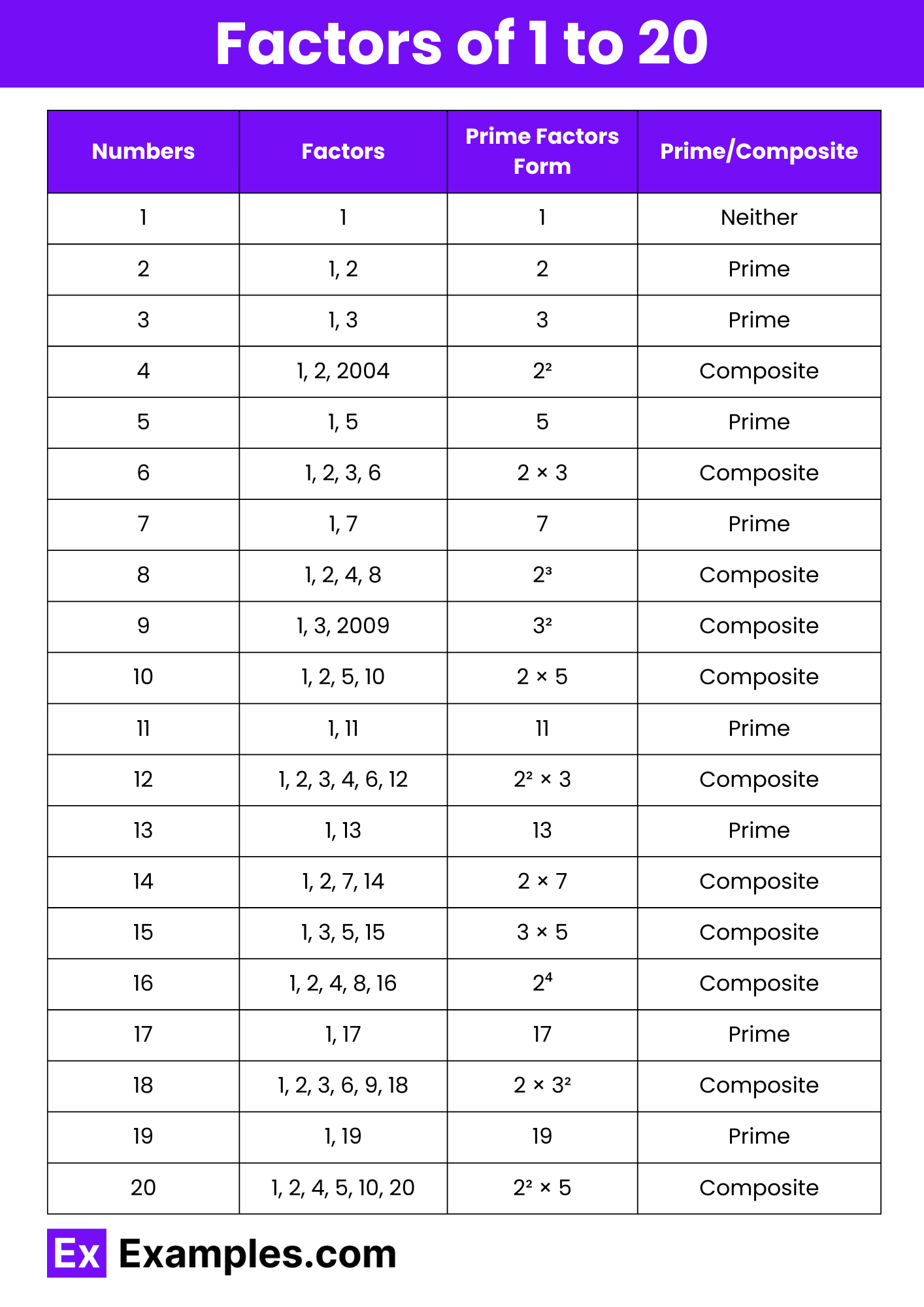
Have you ever wondered about the hidden building blocks of numbers? It's a bit like looking at a wall and figuring out which bricks were used to build it. When we talk about numbers, these special bricks are called "factors." Understanding them is pretty cool, and it helps with all sorts of math puzzles. Today, we're going to really look closely at the number 20, figuring out all the numbers that make it up when you multiply them together or divide into it perfectly.

Learning about factors, especially for a number like 20, gives you a strong base for lots of math ideas. It's not just about remembering a list of numbers; it's about seeing how numbers connect and how they break down. This idea, you know, is really important for things like fractions, algebra, and even some everyday figuring.

So, get ready to explore what makes 20 tick. We'll go through what a factor actually means, how you can find them for any number, and then, we'll clearly lay out all the factors for 20. It's a straightforward path to understanding a basic but really useful math concept, and it's quite a bit simpler than it might sound at first.

• Ilhan Omar Net Worth
• Shia Labeouf Net Worth
• Timothee Chalamet Net Worth

Table of Contents

• What is a Factor, Anyway?
• How Do You Find the Factors of a Number?
  • The Division Method
  • The Multiplication Method
• The Factors of 20 Revealed
  • Factor Pairs for 20
• Prime Factors of 20
• Common Factors with 20
• Why Do Factors Matter?
• Frequently Asked Questions About Factors of 20
• Wrapping Things Up

What is a Factor, Anyway?

When we talk about a "factor" in math, we're talking about a number that can split another number perfectly, leaving nothing leftover. It's like sharing a pie equally among friends; everyone gets a full piece, and there are no crumbs left on the plate. My text explains it well, saying, "A factor of a number is a number that divides the given number evenly or exactly, leaving no remainder." This means if you divide the original number by one of its factors, the answer will be a whole number, and you won't have any bits left over.

You can also think of factors as the numbers you put together with multiplication. My text notes, "Factors are the numbers you multiply together to get." So, if you have two numbers that multiply to make a third number, those first two numbers are factors of the third. For example, with the number 12, my text points out that "3 and 6 are factors of 12 because 12" can be made by multiplying them, or by dividing. It's a pretty neat way to see how numbers are built.

Basically, factors are those special numbers that fit perfectly into another number, either through division or by being multiplied together. My text really makes this clear, saying, "A factor of a number divides the given number without any remainder." This simple idea, you know, is the core of what we're looking at today, and it helps us figure out the components of numbers like 20.

• Brett Favre Net Worth
• Daymond John Net Worth
• Danny Devito Net Worth

How Do You Find the Factors of a Number?

Figuring out the factors of a number, like 20, is actually quite simple once you get the hang of it. My text mentions, "How to find factors of a number, Explore with definition, methods, examples & solutions." There are a couple of main ways to approach this, and both are pretty straightforward. We'll look at the division method and the multiplication method, which basically cover all your bases.

It's all about finding those pairs of numbers that either divide perfectly or multiply to give you the number you're working with. You can, for instance, start with the smallest possible factor and work your way up. This systematic approach helps make sure you don't miss any of the numbers that fit the bill.

Remember, when studying factors, we typically focus on positive whole numbers. My text says, "For positive integers the calculator will only," which suggests we usually stick to positive numbers in this context. This makes the process a bit less complicated and easier to manage, too it's almost a given in basic math.

The Division Method

One common way to find factors is by trying to divide the number by smaller whole numbers, starting from 1. If the division results in a whole number with no remainder, then both the number you divided by and the answer to that division are factors. For example, if you divide 20 by 1, you get 20, so 1 and 20 are factors. My text notes, "The factors of a number are all the numbers that divide that number." This method really highlights that idea.

You keep trying numbers, moving up one by one. So, you'd try 2, then 3, then 4, and so on, up to the square root of the number you're factoring. If you try a number and it leaves a remainder, it's not a factor. This systematic check, you know, helps you find every single one without much fuss.

It's a pretty reliable way to find all the numbers that can split your target number perfectly. This approach, in fact, helps you really see the relationship between division and factors, which is a fundamental connection in mathematics. You are, in a way, just testing out all the possibilities.

The Multiplication Method

The multiplication method is, in some respects, the flip side of the division method. Here, you think about which pairs of numbers, when multiplied together, give you the original number. My text points out, "Factors can also be seen as pairs of numbers that..." This is exactly what we're doing here. You start with 1 and think, "What do I multiply 1 by to get my number?" Then you move to 2, and so on.

For instance, if you're looking for factors of 20, you'd think:

• 1 times what equals 20? (1 x 20 = 20)
• 2 times what equals 20? (2 x 10 = 20)
• 3 times what equals 20? (No whole number)
• 4 times what equals 20? (4 x 5 = 20)

You keep going until the numbers you are trying to multiply start repeating or crossing over. This method, naturally, also helps you find all the factor pairs, which is quite useful.

My text says, "Factors in math refer to a number, or numbers, that produce a given number when multiplied." This method really brings that definition to life, allowing you to build the number from its foundational parts. It's a very visual and intuitive way to understand factors, you know, by seeing them as building blocks.

The Factors of 20 Revealed

Alright, so let's apply these methods to our target number: 20. We're looking for all the positive whole numbers that can divide 20 without leaving any remainder. We're also looking for pairs of numbers that multiply together to make 20. It's a straightforward process, and you'll see the complete list pretty quickly.

Starting with the smallest positive whole number, 1, and working our way up, we can systematically discover each factor. This approach ensures we don't miss any of the numbers that fit the definition. It's a bit like checking off a list, making sure every possibility is covered, which is quite helpful.

So, after doing our checks, the numbers that divide 20 perfectly are: 1, 2, 4, 5, 10, and 20. These are the factors of 20. My text mentions, "The whole number factors of 12 are 1, 2, 3, 4, 6, and 12," which gives a similar example for another number. It really shows how this concept works across different numbers.

Factor Pairs for 20

When we find factors, we often find them in pairs. These are the two numbers that, when multiplied, give you the original number. My text notes, "Factors can also be seen as pairs of numbers that..." This is a great way to think about them. For 20, these pairs are pretty easy to spot once you have the list of individual factors.

Here are the factor pairs for 20:

• 1 and 20 (because 1 x 20 = 20)
• 2 and 10 (because 2 x 10 = 20)
• 4 and 5 (because 4 x 5 = 20)

Notice that once you get to 4 and 5, if you continued, you'd just be reversing the pairs (like 5 and 4). So, you know, these three pairs cover all the bases for 20.

These pairs, in fact, really illustrate the multiplication aspect of factors. They show you exactly which numbers, when working together, construct the number 20. It's a clear way to see the building blocks in action, and it's quite simple to understand.

Prime Factors of 20

Now that we know all the factors of 20, let's talk about a special kind of factor: prime factors. A prime number is a whole number greater than 1 that only has two factors: 1 and itself. Think of numbers like 2, 3, 5, 7, and so on. My text mentions, "Learn all about prime factors up to 100 in this engaging video lesson for kids," which hints at their importance.

To find the prime factors of 20, you basically break 20 down into its smallest prime building blocks. You start dividing 20 by the smallest prime number possible, which is 2.

• 20 ÷ 2 = 10
• 10 ÷ 2 = 5

Now, 5 is a prime number itself, so you stop there. This means the prime factors of 20 are 2, 2, and 5. When you multiply these together (2 x 2 x 5), you get 20. This process, you know, is called prime factorization, and it's pretty neat.

Understanding prime factors is, in a way, getting to the absolute core components of a number. It's like finding the atoms that make up a molecule. This idea is really fundamental in number theory and comes up quite often in more advanced math topics, so it's good to have a grasp on it.

Common Factors with 20

Sometimes, we need to find factors that two or more numbers share. These are called common factors. It's like finding what two different numbers have in common in terms of their building blocks. My text gives a great example, stating, "The factors of 20 that are also factors of 30, or the common factors of 20 and 30, are 1, 2, 5, and 10." This really shows how the concept works.

To find common factors, you first list all the factors for each number. Let's use the example from my text and list the factors for 20 and 30.

• Factors of 20: 1, 2, 4, 5, 10, 20
• Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30

Then, you look for the numbers that appear in both lists. In this case, those numbers are 1, 2, 5, and 10. These, you know, are the common factors of 20 and 30.

This skill of finding common factors is quite useful, especially when you're working with fractions and need to simplify them, or when you're finding the greatest common factor (GCF), which is the largest number that divides both numbers perfectly. It's a pretty practical application of what we've been discussing, and it shows how these ideas connect in different math situations.

Why Do Factors Matter?

You might be wondering why it's such a big deal to know the factors of a number like 20. Well, understanding factors is actually a foundational skill that helps with a lot of other math concepts. It's not just a standalone topic; it's a building block for so much more. My text mentions, "Learn all about factors and their applications in problems here!" which really highlights their practical use.

For example, when you're simplifying fractions, you're essentially looking for common factors in the top and bottom numbers to make the fraction smaller and easier to work with. If you didn't know about factors, that would be a much harder task. It's also super important for finding the greatest common factor (GCF) and the least common multiple (LCM), which are key in solving many math problems, especially those involving ratios and proportions. This knowledge, you know, truly opens up new ways to solve things.

Beyond schoolwork, the idea of breaking things down into their components, which is what factoring is all about, shows up in many areas. Think about how a manufacturing process breaks down a product into its parts, or how a computer program uses smaller functions to build a larger one. The basic principle of understanding how things are composed is, in a way, rooted in this simple math concept. It's a pretty powerful idea, honestly, even if it seems basic at first glance. You can learn more about prime factorization, for instance, which builds on these factor ideas.

Knowing factors also helps you get a better feel for numbers themselves. It makes you see their relationships and how they interact. This deeper understanding can make math less intimidating and more like a puzzle you can solve. My text mentions, "Here you’ll learn about factors, including recognizing factors, the commutative property, how to find all factor pairs of a given number, and solving problems using factors." This really captures the breadth of what you gain.

It's also a skill that helps with mental math. If you know the factors of numbers well, you can often do calculations faster in your head. For example, if you need to divide 20 by something, knowing its factors immediately gives you the possible whole number answers. This, you know, can save you a bit of time and effort.

Furthermore, factoring is a core concept in algebra. When you get to more advanced math, you'll be factoring algebraic expressions, which is just like factoring numbers but with letters and symbols mixed in. The basic principles you learn with numbers like 20 directly apply there. So, in a way, you're building a foundation for future math success just by understanding these simple ideas now. You can learn more about basic math concepts on our site, and also explore how these ideas connect to other areas of mathematics.

Frequently Asked Questions About Factors of 20

People often have a few common questions when they're figuring out factors, especially for a number like 20. Let's clear up some of those common points, as they tend to pop up quite a bit. It's good to get these sorted out so you can feel really confident about your understanding.

What are the prime factors of 20?

The prime factors of 20 are 2 and 5. When you break 20 down into its prime building blocks, you find that 20 equals 2 multiplied by 2, and then multiplied by 5 (2 x 2 x 5 = 20). So, the unique prime numbers that make up 20 are 2 and 5. It's a pretty straightforward way to look at its fundamental components.

How do you find the factors of any number?

To find the factors of any number, you can use either the division method or the multiplication method. For the division method, you test every whole number from 1 up to the square root of your number. If a number divides evenly with no remainder, then both the divisor and the result of the division are factors. For the multiplication method, you list pairs of numbers that multiply together to give you your original number. You start with 1 times the number itself, then 2 times whatever gives you the number, and so on, until you start repeating pairs. This way, you know, you'll catch them all.

What are common factors?

Common factors are the numbers that two or more different numbers share as their factors. For example, if you list all the factors of 20 (1, 2, 4, 5, 10, 20) and all the factors of 30 (1, 2, 3, 5, 6, 10, 15, 30), the numbers that appear in both lists are the common factors. For 20 and 30, these common factors are 1, 2, 5, and 10. It's like finding the shared building blocks between different numbers, which is pretty neat.

Wrapping Things Up

We've taken a good look at the factors of 20, breaking down what factors are and how you can find them. We saw that factors are numbers that divide another number perfectly, leaving no remainder, or numbers that multiply together to create that number. For 20, these special numbers are 1, 2, 4, 5, 10, and 20. We also explored factor pairs, prime factors, and how to find common factors, using 20 as our main example. This, you know, really gives a full picture.

Understanding factors is more than just a math exercise; it's a way to see the underlying structure of numbers. This skill helps build a strong foundation for many other math topics you'll encounter, from fractions to algebra. So, the next time you see the number 20, you'll know a lot more about its numerical makeup. Keep exploring numbers, and you'll find they have many interesting stories to tell!