Have you ever found yourself wondering about distances, perhaps how far a bird flies, or the vastness of space? Well, it's almost a given that at some point, you'll encounter distances measured in kilometers, and then, just like that, you might need to think about them in meters. This simple shift, going from kilometers to meters, is actually pretty fundamental to understanding our world, and it comes up in more places than you might initially imagine. We see it in everyday life, in science, and even in some pretty big calculations about things way out there.

So, understanding how to switch between these two units, km to m, really helps clarify things. It's like having a special lens that lets you see the same distance in a different light, perhaps a more detailed or a more manageable way. This conversion is a basic building block for many calculations, whether you're figuring out how fast something is moving or how much space something takes up. It's a skill that, honestly, just makes life a little bit smoother when dealing with measurements.

Today, we're going to explore this very idea, this change from kilometers to meters. We'll look at why it matters, how simple it is to do, and even peek at some real-world examples where this conversion really shines. You know, it's pretty neat how a little number change can make a big difference in how we understand distances, and that's what we're going to get into right now.

• Michael Richards Net Worth
• Ksi Net Worth
• Pete Rose Net Worth

Table of Contents

• The Heart of the Matter: What is a Kilometer and a Meter?
• Why the Switch from km to m Matters
  • Birds in Flight: A Real-World Example
  • Cars on the Road: Keeping Units Consistent
  • Meteoroids and Speed: Understanding Acceleration
  • Measuring the Cosmos: Distances in Space
  • Wind Speed and Daily Life
  • Earth's Crust and Planetary Measurements
• The Simple Steps to Convert km to m
• Common Questions About km to m
• Bringing It All Together: The Value of Conversion

The Heart of the Matter: What is a Kilometer and a Meter?

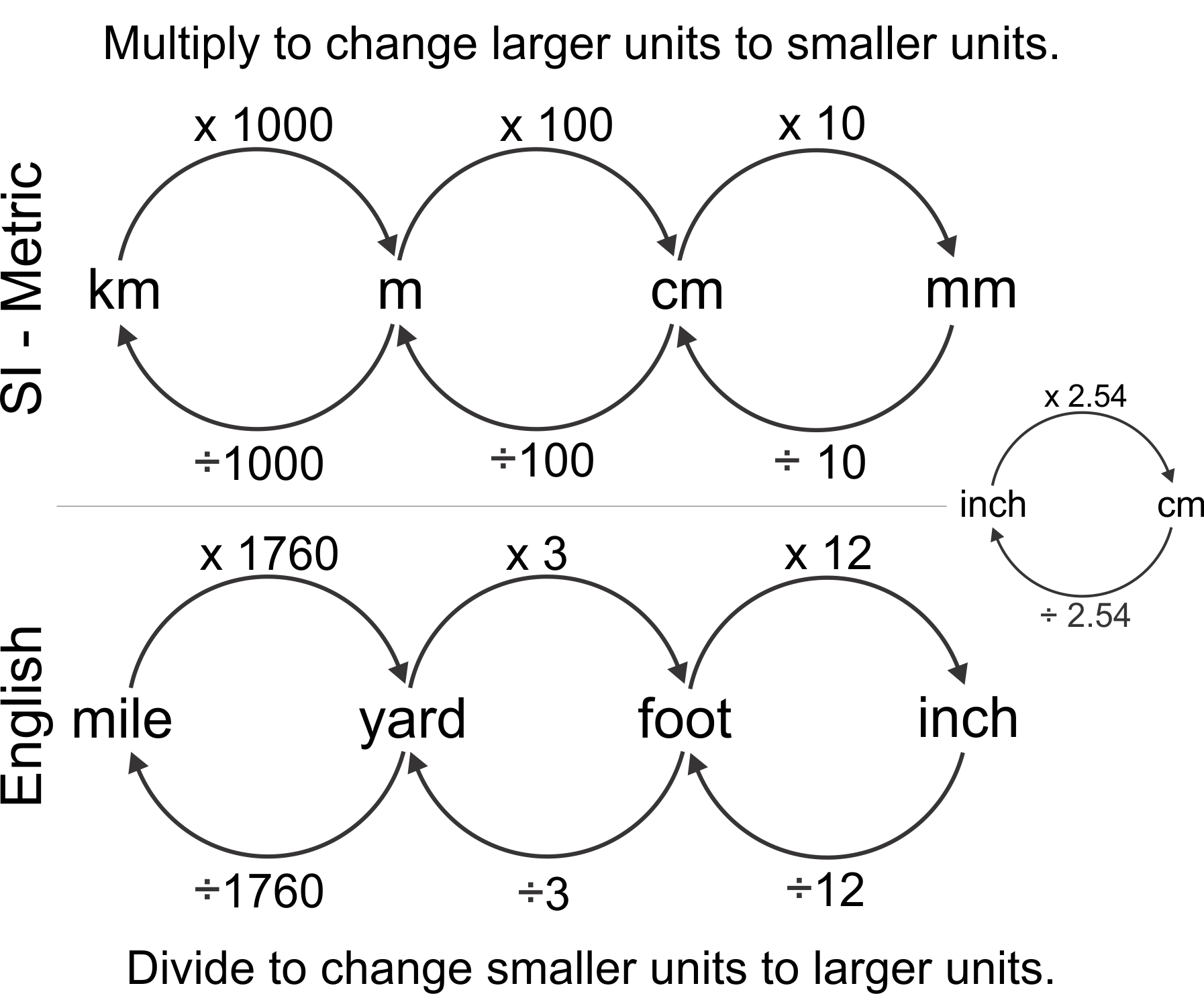
When we talk about measuring distance, we often use units like kilometers and meters. These are part of the metric system, which is used by most of the world, you know. A meter is the basic unit of length in this system. It's, like, a pretty standard length, roughly the distance of a big step for an adult, or a little over three feet. This unit serves as the foundation for many other measurements, too it's almost like the building block for distance.

Now, a kilometer is simply a larger unit of distance that builds upon the meter. The prefix "kilo-" means one thousand. So, when you put "kilo" in front of "meter," you get a kilometer, which means one thousand meters. It's a straightforward relationship, really. This makes longer distances, like the length of a road or the distance between cities, much easier to talk about without using very, very large numbers. For instance, instead of saying "five thousand meters," we can just say "five kilometers," which is much more convenient.

This relationship, that one kilometer is equal to one thousand meters, is the key to converting between the two. It's a fixed value, always true, and it makes the process of changing from km to m incredibly simple. Knowing this little fact is, in a way, like having a secret decoder ring for distances. It allows us to scale our measurements up or down depending on what we need to describe, whether it's a short jog or a cross-country trip.

• Matt Damon Net Worth
• Gucci Mane Net Worth
• Russell Wilson Net Worth

Why the Switch from km to m Matters

Converting kilometers to meters isn't just a classroom exercise; it's something that shows up in all sorts of real-world situations, actually. Sometimes, a distance might seem quite large in kilometers, but when you convert it to meters, it gives you a better sense of scale, especially for things that happen on a smaller, more immediate level. It's about choosing the right tool for the job, you know, picking the unit that best fits the situation at hand. We often see this need for conversion in science, sports, and even just figuring out how long something might take.

For example, when you're dealing with very precise calculations, or when you need to combine distance with other units like time or speed, having everything in a consistent unit, like meters, becomes really important. This consistency helps prevent errors and makes calculations much clearer. It's kind of like making sure all your ingredients are measured in the same way when you're baking; it just makes the whole process work better. Let's look at some specific instances where this conversion truly proves its worth.

Birds in Flight: A Real-World Example

Imagine a bird, soaring through the sky, covering a good distance. Let's say, just for argument's sake, this bird can fly 30 kilometers in one hour. Now, if you want to figure out how far that bird flies in meters, or perhaps how long it takes to cover a certain number of meters, converting the kilometers to meters becomes very helpful. My text shows us exactly this: "30 km = 30,000 m." This tells us that the bird can cover 30,000 meters in one hour, which is a lot of meters, naturally.

This conversion is not just for curiosity; it has practical implications. If you then want to know how long it takes the bird to fly, say, 22,000 meters, having the original speed in meters per hour makes the calculation straightforward. My text also gives us this: "the bird can fly 22,000 meters in (22000 / 30000) * 60 mins = 44 mins." See, by first converting the 30 km to 30,000 m, the calculation for time becomes very clear and easy to follow. It allows for a precise timing, which is pretty neat.

So, you see, for things like flight duration or speed over shorter distances, converting from kilometers to meters gives us a much more granular view. It helps us break down larger movements into smaller, more understandable segments, which is really useful for things like flight planning or even just appreciating the impressive capabilities of animals. It's a way of making big numbers a bit more manageable, you know, for practical purposes.

Cars on the Road: Keeping Units Consistent

Think about cars driving on a road, perhaps one car trying to catch up to another. If one car is, let's say, 6 kilometers ahead, and you need to calculate the time it will take for the second car to close that gap, it's often best to have all your distance measurements in the same unit. My text provides a great illustration of this: "So it will be best to convert the 6 km to meters, 6km ⋅ 1000m 1km = 6000m now we can find the time for the 2nd car to catch." This clearly shows why converting km to m is a smart move.

When you're dealing with speeds that are often given in meters per second (m/s) or if other parts of your calculation involve meters, having the initial distance in meters makes the whole problem consistent. It removes the need for extra conversion steps later on and reduces the chance of making a mistake. It's like getting all your ducks in a row before you start a big project, right? This uniformity in units is, frankly, a golden rule in many areas of science and engineering.

So, whether you're trying to figure out how long it takes for one vehicle to reach another, or calculating braking distances, having distances expressed in meters just simplifies the process. It's a pretty practical step that ensures accuracy and makes the numbers line up nicely, which is, you know, exactly what you want when you're trying to solve a problem involving movement. This consistency really helps in getting the right answers.

Meteoroids and Speed: Understanding Acceleration

Consider something as dramatic as a meteoroid changing its velocity. My text mentions, "A meteoroid changed velocity from 10 km/s to 1.8 km/s in 0.03 seconds." While the velocities here are given in kilometers per second, if you were to calculate its acceleration in standard SI units, you'd typically want to work with meters per second. This means converting those kilometer-per-second values into meter-per-second values, which is, arguably, a very common practice in physics.

For instance, 10 km/s becomes 10,000 m/s, and 1.8 km/s becomes 1,800 m/s. This conversion allows you to directly apply formulas that rely on meters as the base unit for distance. When you're calculating acceleration, which is the change in velocity over time, having the velocity in meters per second makes the final acceleration unit (meters per second squared, or m/s²) perfectly standard. It just makes the numbers work out in a way that's universally understood, basically.

So, even in high-speed, cosmic scenarios, the principle of converting km to m, or km/s to m/s, holds true. It ensures that your calculations are robust and that your results can be easily compared with other scientific data. It's a foundational step in many scientific problems, really, allowing us to accurately describe incredibly fast and powerful events. This unit consistency is, in fact, absolutely critical for precise scientific work.

Measuring the Cosmos: Distances in Space

When we look out into space, the distances involved are truly mind-boggling. My text talks about "Z = 149 million km the distance to an object in space." That's an enormous number in kilometers already, but imagine trying to express that in meters! While we typically use kilometers or even light-years for such vast distances to keep the numbers manageable, the underlying principle of conversion still applies. You could, in theory, convert 149 million kilometers to an even more staggering number of meters, which would be 149,000,000,000,000 meters. That's a lot of zeros, obviously.

Even though we don't usually express cosmic distances in meters because the numbers become unwieldy, the ability to make that conversion highlights the sheer scale we're talking about. It reinforces the idea that kilometers are just a convenient way to represent many thousands of meters. It also shows how the metric system scales so beautifully, from the very small to the incredibly vast, just by changing a prefix, you know.

This idea of scaling units, even if not always performed for practical reasons in space, helps us appreciate the consistent nature of measurement. It's a reminder that all these units are interconnected and can be transformed into one another, depending on the context and the precision needed. It's pretty fascinating how a simple conversion rule can apply to something as immense as the distance to a celestial body, in a way.

Wind Speed and Daily Life

Even in everyday situations, like checking the weather, you might encounter units that benefit from conversion. My text mentions, "I get that the wind comes from the south west quadrant, blowing at a speed of 3 mps (11 km/h)." Here, we see wind speed given in both meters per second (mps) and kilometers per hour (km/h). While these are different rates, the fact that 11 km/h is mentioned alongside 3 mps shows a direct relationship that involves converting distance units.

To go from kilometers per hour to meters per second, you first need to convert the kilometers to meters and the hours to seconds. So, 11 kilometers becomes 11,000 meters. Then, one hour becomes 3600 seconds. This allows you to perform the calculation to get meters per second. This is a very common conversion for things like weather forecasting, sports analysis, or even just understanding how fast the wind is truly blowing around you. It's a practical application that many people might use without even realizing it, sort of.

So, whether you're trying to understand how quickly a storm is approaching or how fast a runner is moving, being able to switch between kilometers and meters, even within a larger unit like speed, is a really useful skill. It helps make sense of the numbers and puts them into a more relatable context. This ability to convert is, frankly, quite empowering for understanding the world around us.

Earth's Crust and Planetary Measurements

When we talk about the Earth itself, particularly its structure, units of measurement are, of course, very important. My text touches on this: "How do you estimate the average bulk modulus of earth's crust given that the density of rock is about 2400 kg/m3." Here, density is given in kilograms per cubic meter (kg/m³), which uses meters as its base length unit. If you were to discuss the thickness of the crust, it might be given in kilometers, like "49.3 km" for the radius of a sphere of solid nitrogen mentioned later in my text.

The fact that density is in kg/m³ means that any calculations involving volume for the crust would naturally use meters. If you have a measurement like the thickness of the crust in kilometers, you'd convert it to meters to maintain consistency with the density unit. So, 49.3 km would become 49,300 meters. This ensures that all parts of your calculation are speaking the same "unit language," which is pretty crucial for accurate scientific modeling, you know.

This consistency is not just about convenience; it's about accuracy in scientific calculations. Whether you're estimating the properties of Earth's interior or the size of a hypothetical sphere, ensuring all your length measurements are in meters when other related units (like density) are also meter-based is a fundamental step. It's a basic principle that underpins a lot of serious scientific work, and it's, in a way, very important for getting reliable results.

The Simple Steps to Convert km to m

Converting kilometers to meters is, thankfully, one of the simplest conversions you'll ever do. It all boils down to that one key relationship we talked about earlier: 1 kilometer equals 1,000 meters. So, to turn any number of kilometers into meters, you just need to multiply that number by 1,000. It's really that straightforward, honestly.

Let's take an example from my text: "30 km = 30,000 m." Here, you take the 30 kilometers and multiply it by 1,000. So, 30 * 1,000 = 30,000. That gives you 30,000 meters. It's just adding three zeros to the end of the kilometer number, or moving the decimal point three places to the right. This makes it a quick mental calculation for many numbers, which is pretty handy.

Another example from my text is "6km ⋅ 1000m 1km = 6000m." This shows the same process. You have 6 kilometers, and you multiply it by 1,000 to get 6,000 meters. This method works every single time, no matter how many kilometers you're dealing with. It's a very reliable way to make sure your distance measurements are consistent, and it's, like, a fundamental rule of the metric system.

So, the rule is always the same:

1. Start with the number of kilometers you have.
2. Multiply that number by 1,000.
3. The result is your distance in meters.

It's a simple multiplication, and it's something you can do quickly whether you're using a calculator or just doing it in your head. This ease of conversion is one of the big advantages of the metric system, you know, making it very user-friendly for all sorts of applications.

Common Questions About km to m

How many meters are in a kilometer?

There are exactly 1,000 meters in one kilometer. This is a fixed conversion factor, which means it never changes, you know. The prefix "kilo-" always means "one thousand" in the metric system, so a kilometer is simply a thousand meters. This makes the conversion very consistent and easy to remember, which is pretty helpful for quick calculations.

Why do we convert km to m?

We convert kilometers to meters for several important reasons, actually. Sometimes, it's about consistency in calculations, especially in science and engineering, where other units (like speed in meters per second) require meters as the base. Other times, it's about scale; meters give a more detailed or manageable number for shorter distances, making them easier to visualize or use in specific contexts. It just helps to have the right unit for the job, you know, to make things clearer.

Is it always 1000 meters per kilometer?

Yes, it is always 1,000 meters per kilometer. This is a fundamental definition within the International System of Units (SI), which is the modern form of the metric system. There's no variation or exception to this rule. It's a standard that ensures everyone using these units gets the same results, which is, in fact, a cornerstone of global scientific and commercial communication. You can always count on this relationship, pretty much.

Bringing It All Together: The Value of Conversion

So, as we've seen, the simple act of converting kilometers to meters is far more than just a math exercise. It's a practical skill that helps us make sense of the world around us, from understanding how far a bird can fly in a given time, as my text points out with "30 km = 30,000 m," to calculating how quickly one car might catch another, where "6km ⋅ 1000m 1km = 6000m" becomes really useful. This conversion allows us to pick the right unit for the right situation, making our measurements and calculations more accurate and easier to grasp.

Whether you're dealing with vast distances in space, like "Z = 149 million km," or more immediate measurements like wind speed, the ability to switch between kilometers and meters is a powerful tool. It helps us ensure consistency in scientific formulas, like those for meteoroid acceleration, and gives us a better sense of scale for everything from planetary crusts to the flight path of an animal. It's a foundational concept that, frankly, just makes life with numbers a little bit simpler and more precise.

So, the next time you see a distance in kilometers, just remember that a quick multiplication by 1,000 can turn it into meters, giving you a fresh perspective on the measurement. This simple conversion is a gateway to a deeper appreciation of distances, big or small, and it's a skill that will, you know, serve you well in many different contexts. Keep practicing, and you'll find yourself converting like a pro in no time! Learn more about the International System of Units on our site, and link to this page for more helpful tips.